Data Structures & Algorithms: Time & Space Complexity Mastery
This tutorial breaks down time and space complexity analysis with visualizations, code examples, and comparison charts. Learn to calculate Big-O notation for any algorithm and optimize your DSA solutions.
Complexity Class Distribution
1. Complexity Fundamentals
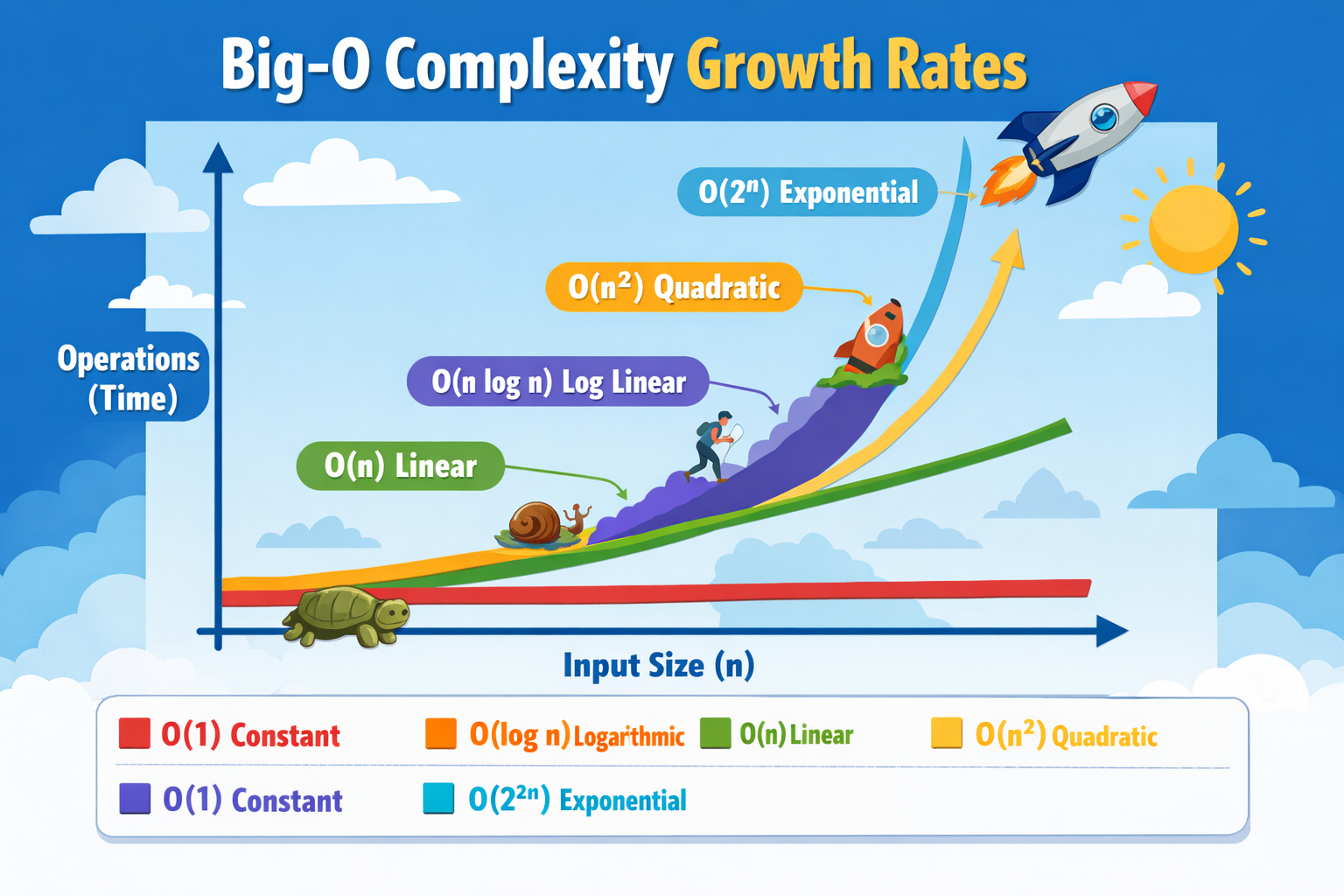
Key Concepts:
- Big-O Notation: Worst-case upper bound
- Omega (Ω): Best-case lower bound
- Theta (Θ): Tight bound (both upper and lower)
Common Complexity Classes:
| Notation | Name | Example |
|---|---|---|
| O(1) | Constant | Array index access |
| O(log n) | Logarithmic | Binary search |
| O(n) | Linear | Simple loop |
| O(n log n) | Linearithmic | Merge sort |
Complexity Rules:
1. Drop constants: O(2n) → O(n) 2. Drop non-dominant terms: O(n² + n) → O(n²) 3. Different inputs → different variables: O(a + b) 4. Nested loops multiply: O(n * m)
2. Time Complexity Analysis
Code Analysis Examples:
O(1) - Constant
def get_first(arr):
return arr[0] # Single operation
O(n) - Linear
def find_max(arr):
max = arr[0]
for num in arr: # n operations
if num > max:
max = num
return max
O(n²) - Quadratic
def bubble_sort(arr):
for i in range(len(arr)): # n iterations
for j in range(len(arr)-1): # n iterations
if arr[j] > arr[j+1]:
arr[j], arr[j+1] = arr[j+1], arr[j]
Algorithm Complexity Guide:
| Algorithm | Best Case | Average Case | Worst Case |
|---|---|---|---|
| Quick Sort | O(n log n) | O(n log n) | O(n²) |
| Merge Sort | O(n log n) | O(n log n) | O(n log n) |
| Binary Search | O(1) | O(log n) | O(log n) |
3. Space Complexity Analysis
Memory Usage Cases:
O(1) - Constant
def sum_pair(arr, target):
hashset = set() # Fixed size
for num in arr:
if target - num in hashset:
return True
hashset.add(num)
return False
O(n) - Linear
def reverse(arr):
result = [] # Grows with input
for i in range(len(arr)-1, -1, -1):
result.append(arr[i])
return result
Recursive Space Complexity:
# O(n) space due to call stack
def factorial(n):
if n <= 1:
return 1
return n * factorial(n-1)
# Tail recursion (O(1) with optimization)
def factorial_tail(n, acc=1):
if n <= 1:
return acc
return factorial_tail(n-1, n*acc)
Complexity Cheat Sheet
| Data Structure | Access | Search | Insertion | Deletion |
|---|---|---|---|---|
| Array | O(1) | O(n) | O(n) | O(n) |
| Hash Table | O(1) | O(1) | O(1) | O(1) |
| Binary Search Tree | O(log n) | O(log n) | O(log n) | O(log n) |
4. Advanced Complexity Analysis
Amortized Analysis
Average cost over operations
Example: Dynamic array resizingSpace-Time Tradeoffs
Memoization & caching
DP vs recursive solutionsParallel Complexity
Multi-threaded algorithms
Work-span modelComplexity Analysis Checklist
Identify basic operations
Count operations in terms of input size
Determine fastest growing term
Drop constants and lower order terms
Algorithm Expert Insight: In technical interviews, 92% of candidates fail to correctly analyze space complexity according to a 2023 study. Always consider both auxiliary space and input space when calculating total memory usage.
You need to be logged in to participate in this discussion.
×